# I can learn hard things (and so can you)

I've learned that I can learn hard things these past few months. Not just me, all of us. Or, shall I say: "We can learn hard things" like Glennon Doyle's We Can Do Hard Things (opens new window)?

Somewhere along the line in university, I lost the confidence that I could learn difficult topics. Even though I studied mathematics and computer science and got good grades, I noticed the top students and thought they had some abilities I didn't have. I thought I could never know as much as they did or learn the things they could.

Now, I think I could (maybe). It might just take me a little longer.

Long ago, I read that confidence comes from actually doing the thing you're trying to be more confident in. This leads to a paradox because you need at least some confidence to start doing the thing.

Nevertheless, the tiniest amount of blind confidence or at least a little hope can get you going. You can start with the babiest of steps.

My journey back into learning hard things started with the AWS Solutions Architect Associate course that my former manager recommended (probably semi-required). I created a spreadsheet of the topics covered in the exam and the chapters in the course. I wondered how I'd ever get through them all.

Below, you can see the spreadsheets mentioned above I created.

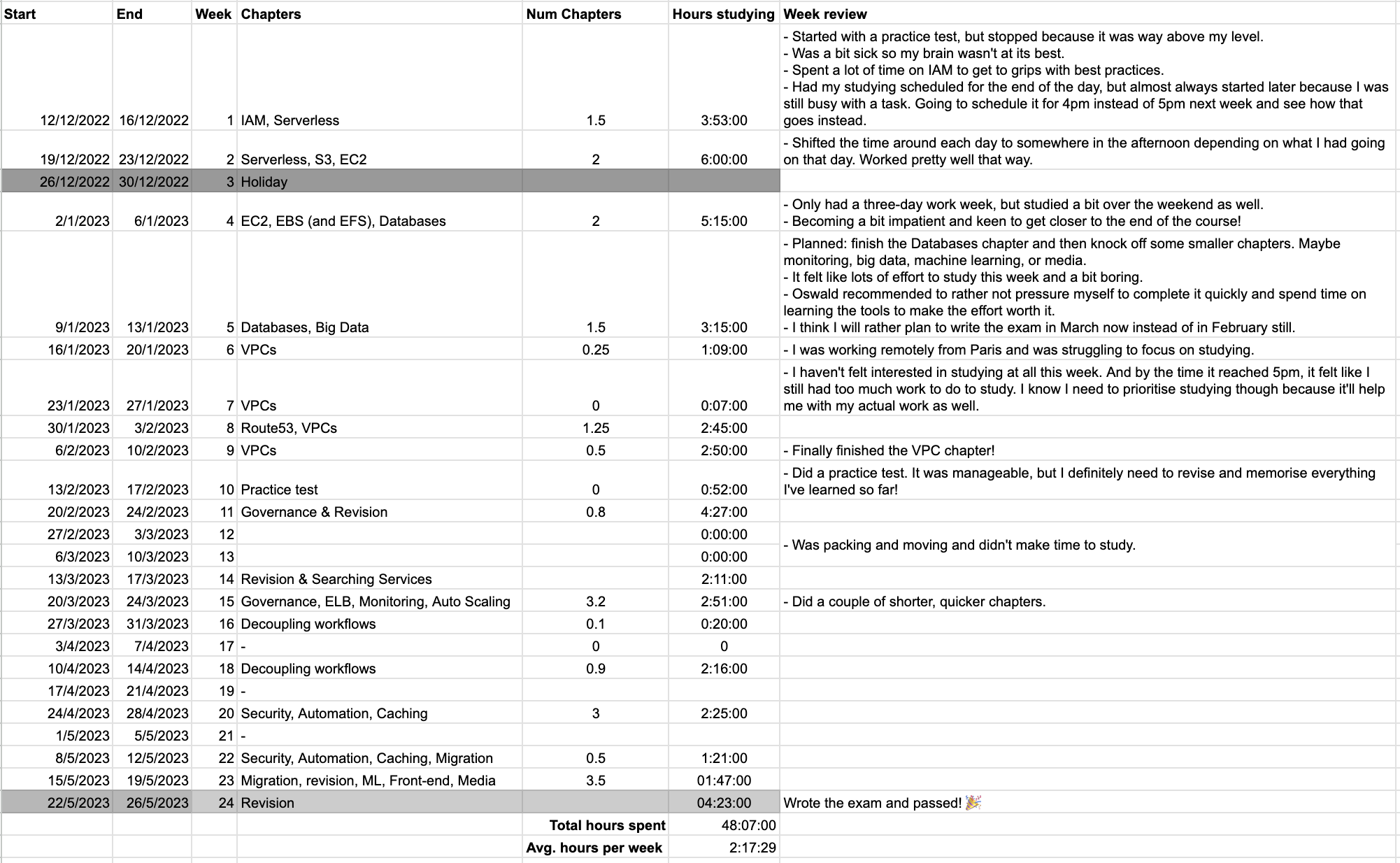
I somehow managed to keep on studying even though I had sometimes gone off-track. Six months later, I finally wrote the exam.

That momentum pushed me to write the Solutions Architect Professional and the Security exams later in the year. Since these courses focused more on memorisation than reasoning, I wanted to see if I could carry this pattern into a more reasoning-focused course. I did one of the QBronze (opens new window) courses as an introduction to quantum computing.

This course challenged me. I almost gave up a few times, but the first few days' momentum helped me complete the course. To be honest, however, I still don't understand the topic of the last day: Grover's search algorithm. This fact disappointed me for a while, but I decided to let it go and come back to the problem at another time. Sometimes, the passage of time and distance from a problem gives you a fresh perspective. Things might suddenly become apparent when you return to it.

All of this, combined with my nagging desire to do a master's ever since I first graduated from university, led to me studying towards a master's in mathematics this year. I revised my first-year calculus before joining the programme and was shocked that I could not recall very much of it at all.

Nevertheless, I've reached a point where I'm semi-confident in doing integrals again. I've also learned from my lecturers that it is acceptable not to know everything in mathematics. Many researchers focus on a narrow topic and don't necessarily know a lot about the rest of the vast expanse of mathematics.

I'm currently considering fields to research during my research project later this year. It is daunting to consider topics about which I know nothing and imagine that I will need to write (hopefully something useful) about them merely a few months later. However, with my new(re-)found confidence in my learning abilities, I feel up to the task (with some additional positive self-talk). I know that it will just take time, lots of revision, and practice.

I hope that whatever I do after this year, I will carry this passion and momentum of learning. I hope always to dig deeper and understand whatever I'm working with from its first principles.