# My year at the African Institute for Mathematical Sciences (AIMS) in 2025

# Introduction
I'm spending my 2025 doing a master's in mathematical sciences at what is sometimes called (opens new window) Muizenberg's "monastery of mathematics", the African Institute for Mathematical Sciences (AIMS). (opens new window)
The founder of AIMS, Neil Turok, wrote an inspiring article on Nature (opens new window) in 2011 about why he started AIMS in a derelict art-deco hotel in one of Cape Town's seaside suburbs. The institute has since grown to multiple African countries and expanded to providing a master's in AI, in addition to the master's in mathematics.
I joined the mathematics programme in January to expand my mathematical knowledge and skills, and to evaluate whether I should pursue further opportunities in academica. I will be updating this page with summaries of the courses and experiences I've had at AIMS as the year progresses.
# Structure of the programme
The AIMS master's programme (opens new window) is divided into three phases:
- Skills courses,
- Review courses, and
- A research project.
Each course lasts three weeks and we do two courses during each three week block.
# Courses
# Block 1 (13 - 31 January): Two skills courses
# Python
An introduction to Python. Since I've done a lot of Python programming before, I used the time to review some of my undergraduate calculus and linear algebra.
# Mathematical problem-solving
This course focussed on a review of methods for proving mathematical theorems.
Our group's final project considered the "egg drop problem" where a farmer enters a (fictional) competition to test the durability of eggs.
I have to admit that I felt quite a lot of nerdy pleasure at solving some of these seemingly inane mathematical questions.
# Block 2 (3 - 21 February): Two skills courses
This block properly challenged me, because not only had I caught a cold, but I also contended with two subjects which I knew very little about.
# Physics problem-solving
This course discussed approaching broad physics questions, such as: "how long would it take a molecule in the center of a room to reach the edge of the room?" using a problem-solving approach.
This course properly challenged me since I haven't considered a single physics problem since my second-year at university in 2014 (more than ten years ago!).
# Statistical skills
This was my first "real" statistics course ever. I enjoyed the combination of rigorous mathematics, combined with exploration and creativity when it came to presenting and analysing data.
During the last week, we had to submit a group report on the data of one of the UN's Sustainable Goals.
Wackerly, Mendenhall, and Scheaffer's Mathematical Statistics with Applications book helped me immensely during this course.
# Block 3 (3 - 20 March): One skill course and one review course
# SageMath
For this course, we are learning how to use the SageMath (opens new window) programming language (which is based on Python) for mathematical problems. So far, it has not yet been very challenging, but it is good to know what the capabilities of SageMath are. I have found it to be more user-friendly than languages such as R or MATLAB.
# Formal methods for software development
For our very first review course this year, we could decide between:
- Classical mechanics,
- Invariant rings and quotient varieties, or
- Formal methods for software development.
I decided on formal methods for software development, because I didn't do any courses on formal verification during my undergraduate degrees.
In week one, we did a review of the different types of formal methods that exist for software development, including model checking and formal verification. In week two and three, we learned to develop and verify Dafny (opens new window) programs.
Recommended reading: Program Proofs by K. Rustan and M. Leino.
# Generative modeling (audit/DNF)
I considered doing one of the AI stream's courses in generative modeling during this block. I audited the course for the first few days, but realised that it was too ambitious.
Instead, I am learning more about deep learning by myself with 3Blue1Brown's Neural Network playlist (opens new window) and the Understanding Deep Learning book (opens new window).
# Block 4 (24 March - 11 April): Two review courses
Our first block with only review courses. Things are about to start getting more interesting...
# Quantum information
We are covering classical information during week one, i.e. Shannon entropy. During week two and three, we will cover some axioms of quantum mechanics and quantum information.
So far, it's been interesting to see probability theory come up again.
Update on 18 April:
This turned out to be one of the most difficult courses I've ever done. This is what some of my notes ended up looking like:

Recommended reading: Quantum Computation and Quantum Information by Michael A. Nielsen and Isaac L. Chuang (the "bible" of this field).
# Analytical techniques in mathematical biology
I have never done any biology-related course at university before, but I selected this course because I didn't have the prerequisite knowledge required for the third course, Geophysical Fluid Dynamics.
This course will focus on applying models of differential equations to biological systems such as cell growth and the spread of pandemics.
Update on 18 April:
This turned out to be a fun one. The lecturer made it accessible even for those of us who don't have much experience in differential equations. Here's a snippet of my notes of drawing equalibrium points and systems of solutions:
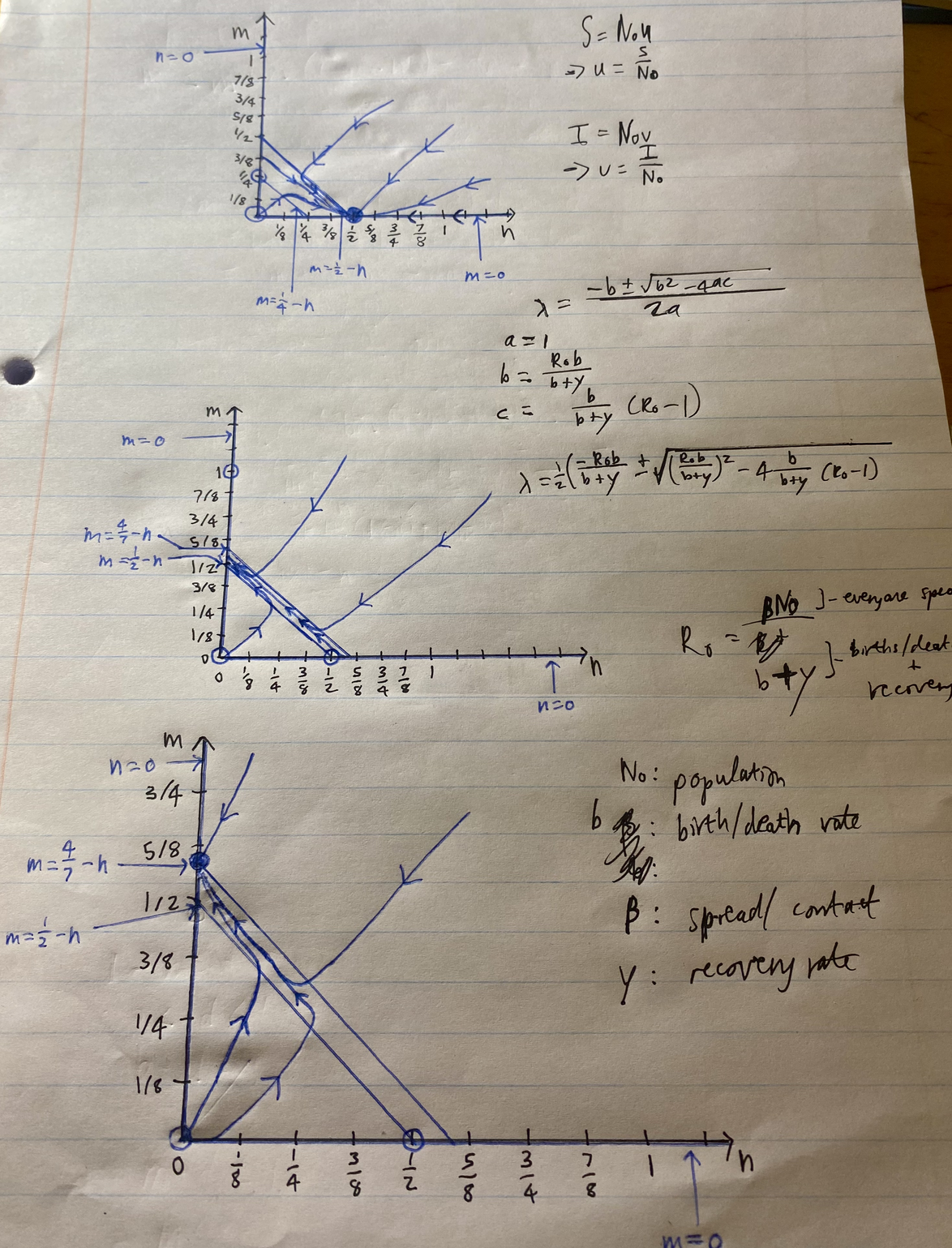
# Block 5 (22 April - 9 May): Two review courses
# Networks
Graph theory and linear algebra for network analysis with practical applications.
We covered a bunch of techniques to analyse graphs and to compare their properties.
I particularly enjoyed applying these techniques to the neuronal network of the Caenorhabditis elegans worm and a food network based on data collected in an estuary in Scotland. The analysis of real-world networks is really what helped to understand the usefulness of it. For example, our analysis of the food network revealed how the extinction of one species could potentially lead to the extinction of other species too.
Recommended reading: Networks by Mark Newman.
# Algebraic systems biology
From The case for algebraic biology: from research to education (opens new window):
If calculus can be an effective tool for tackling biological problems, why not algebra?
The course page freely available here (opens new window).
I enjoyed seeing how boolean models can be used to model the expression of DNA, in particular, the lac operon. I would not have imagined before that biological processes could be modeled to some degree of accuracy by discrete mathematics.
Recommended reading: Chapters 1, 2, and 3 of Mathematical Concepts in Modern Biology by Robeva/Hodge and chapter 6 of Algebraic and Discrete Mathematical Methods for Modern Biology by Robeva.
# Block 6 (12 - 30 May): Two review courses
Two pure mathematics courses this block. I always thought that I would be a pure mathematician if I lived in an era before computers existed - so these three weeks was like a trial run in that different lifetime.
# Model Theory
I had no idea of what Model Theory was before we started the course. Now, I can describe it as:
- The abstract of abstract mathematics.
- Set theory.
- Counting things and comparing infinities.
I especially enjoyed the historical references to the very controversial Axiom of Choice and some pretty neat proof techniques, like Cantor's diagonolisation argument and the "back-and-forth" argument.
# Lie Algebras and Representation Theory
I finally got to experience abstract algebra - and it is, surprise surprise, very abstract indeed. Luckily, in this case, Lie Algebras can be represented in the more familiar objects of matrices.
I've grown to have a fondness for the Lie brackets, the nicheness of the concepts, and the fraktur (opens new window) symbols:
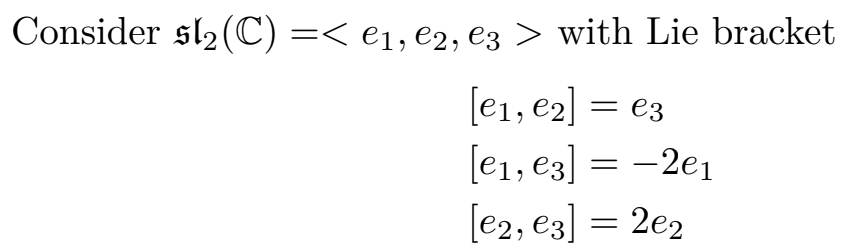
# Block 7 (9 - 27 June): epidemiological modeling workshop
During this block, we attended the three week Meaningful Modeling of Epidemiological Data (MMED) workshop (opens new window). Admittedly, epidemiology is not within my field interest at all. The schedule was intensive - 8:30 to 18:00 every day.
The highlight was when my group consisting of myself and some very enthusiastic fellows from South African Centre for Epidemiological Modelling and Analysis (SACEMA) (opens new window) presented our project on modeling the effectiveness of the measles vaccine.
# Block 8 (30 June - 18 July): One review course
# Hilbert Space Theory
Another pure mathematics course that's quite hard to describe in non-mathematical language, but nevertheless, I absolutely loved this course.
# Project phase (21 July - 23 October)
The topic of my project will be Quantum Cryptography Without One-Way Functions and I will be working with Dr Ryan Sweke on this.
Update on 4 August:
So far, I've studied a bunch of computational complexity and cryptography, mostly through the books "Foundations of Cryptography" by Oded Goldreich, "Introduction to Modern Cryptography" by Jonathan Katz and Yehuda Lindell, and "Computational Complexity" by Sanjeev Arora and Boaz Barak.
On the quantum computing side, I've been reading the "bible" of quantum computing, "Quantum Computing and Quantum Information" by Nielsen and Chuang.
The initial idea of this project was to understand and build on these two papers (one (opens new window) and two (opens new window)) by Kretschmer et al, but after Ryan came across this article (opens new window) we will probably end up focussing on this paper (opens new window) instead.
This article (opens new window) on Quanta Magazine gives a very accessible introduction to some of the core computational complexity ideas that we are looking at.
Update on 12 December:
We ended up focussing on the paper, Founding Quantum Cryptography on Quantum Advantage, or, Towards Cryptography from #𝖯-Hardness (opens new window) by Dakshita Khurana and Kabir Tomer. This talk (opens new window) by Dakshita gives a nice overview of their paper.
This ended up being the notes for what I wrote on the board during my defence:
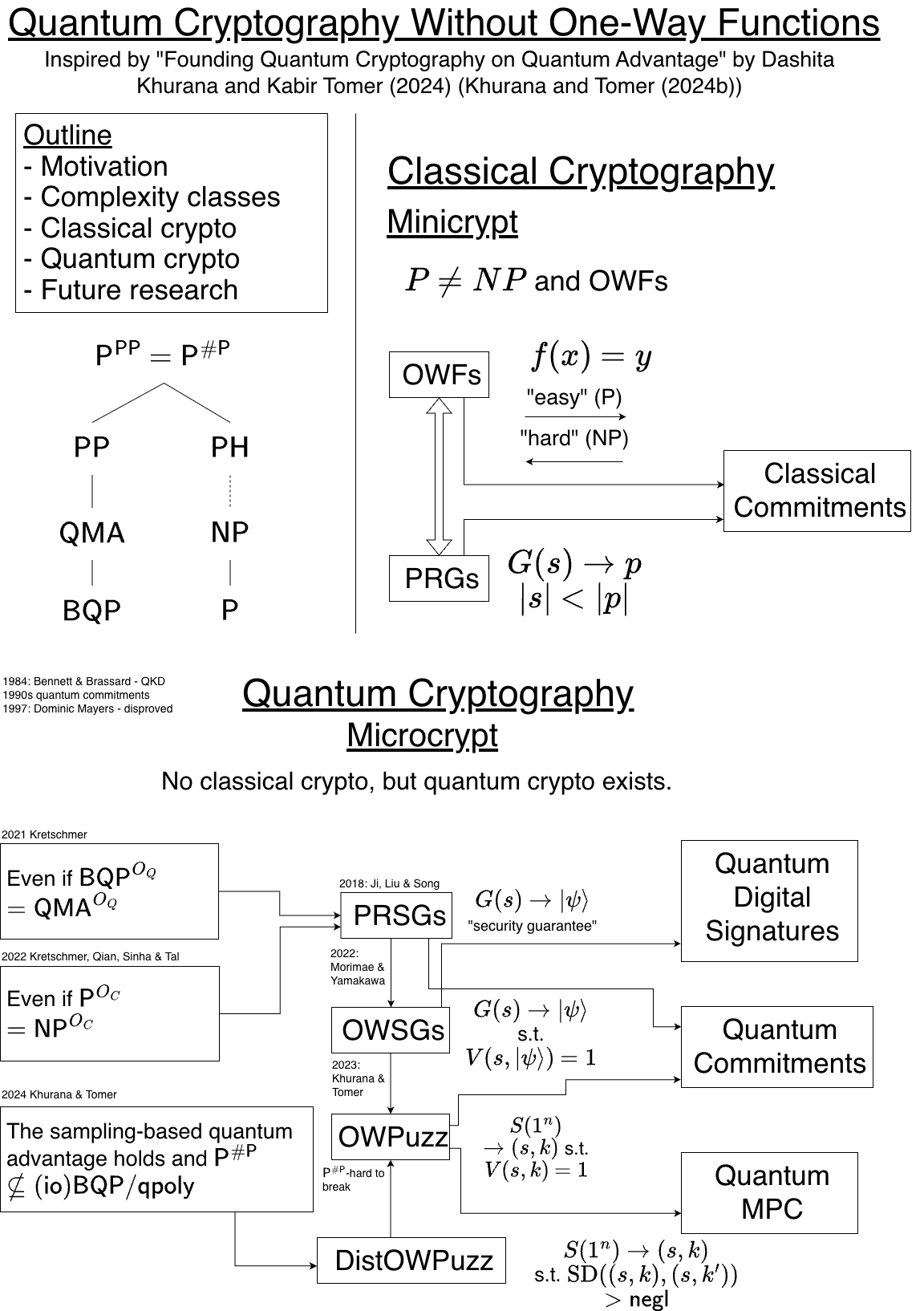
I'm very proud of how far I came in my understanding of this paper and other related ones during the research phase. I definitely got a renewed appreciation of the levels of detail, precision, obscurity, and hardness that these researchers go into in their work!
# Ad-hoc events/lectures
- 15 January 2025: (Future) quantum computing research at AIMS SA by Dr Ryan Sweke.
- 19 February 2025: AIMS Seminar series, 'The fundamental constants at the heart of measurement and physics' by Prof Jean Philiip Uzan.
- 18 March 2025: AIMS Seminar series, 'Computational & systems medicine' by Prof Dr Sara Vieira-Silva
- 17 April 2025: NITheCS & CoRE AI Masterclass, 'A Practical Introduction to Reinforcement Learning' by Prof James Brusey (Coventry University, UK).
- 27 - 30 October 2025: The Theory of Quantum Learning Algorithms workshop.
Thank you for reading my blog! If you enjoyed this post, you're welcome to subscribe via RSS here (opens new window) (I can recommend NetNewsWire on iOS).
